While trying to write down a Perl program that tries to generate XML instances given an XML Schema I stumbled upon the problem of generating instances of xsd:all subtree.
What xsd:all means, basically, is that the listed elements can appear in any order (elements that are listed in an xsd:all can appear 0 or 1 times exactly).
So, in order to do this, the problem reduces to
Create an iterator that returns the next permutation of a given list. Why do I want an iterator?
Consider the following implementation:
sub permute {
my($list)=@_;
return [[]] unless scalar @$list;
my @permutations=();
for(my $i=0; $i<@$list;++$i) {
my @copy_of_list= @$list;
my $removed_list_element = splice(@copy_of_list,$i,1);
push(@permutations, map{[$removed_list_element,@$_]} @{permute(\@copy_of_list)});
}
return \@permutations;
}
The
permute function receives a reference to a list, say,
[ a b c ] and then it returns a list of lists, which is a list of all the permutations of the original list:
[ [a b c] [a c b] [b a c] [b c a] [c a b] [c b a] ].
You can see that for a list with
N items there are
N! permutations.
Note that I'm not discussing lists that contain items that appear more than once. Those actually have less than
N! permutations as disarranging places of similar items is meaningless. For example, the permutations of
[a b a] are: [ [a b a] [ a a b] [b a a] ] because the remaining 3 permutations are the same.
Notice that the number of permutations grows rapidly as
N becomes larger. This makes
permute expensive.
We can try to do less calculations in
permute by understanding that listing all permutations of two lists of the same length, say
N, is actually listing the list of permutations for the list
[0 1 2 ... N-1] and then mapping the elements to the proper positions. Combine this with a cache and we get a speedup whenever we want to permute a list of a length that was already computed before. Note also that once you permute a list of length
N you also permuted lists of length
1 and of length
2 and so on up until
N. So caching also helps when we want to list permutations of smaller lists than computed before.
Let's add a cache to the
permute function:
{
my %cache;
sub permute {
my($list)=@_;
return [[]] unless scalar @$list;
my $key = join ',',@$list;
return $cache{$key} if exists $cache{$key};
my @permutations=();
for(my $i=0; $i<@$list;++$i) {
my @copy_of_list= @$list;
my $removed_list_element = splice(@copy_of_list,$i,1);
push(@permutations, map{[$removed_list_element,@$_]} @{permute(\@copy_of_list)});
}
$cache{$key}=\@permutations;
return \@permutations;
}
}
Our cache is simply a hash. The key to the have is a serialization of the given list elements.
OK, now, but how do we map the elements back onto the list of permutations of indices? Consider the following code:
sub permutmap {
my($original_list,$indices_lists) = @_;
my @list_of_lists;
foreach my $il (@$indices_lists){
my @l;
foreach my $i (@$il) {
push @l,$original_list->[$i];
}
push @list_of_lists,\@l;
}
return \@list_of_lists;
}
Which can similarly be implemented without the explicit loops using
map:
sub mapermute {
my($original_list,$indices_lists) = @_;
return [ map { [map {$original_list->[$_]} @$_] } @$indices_lists ];
}
So all you need now is to feed permute with
1 .. @list and then apply
mapermute or
permutemap on the result.
Still, I have a problem -- there are too many permutations, listing them is expensive, and not necessarily useful (I might not be able to read them all and use them all). It would be great if I could iterate over the permutations until I have enough, and not generate any permutation beyond the ones that I need. This requires a different approach.
I found a few ones such as:
http://www.perlmonks.org/?node_id=29374and
http://www.perlmonks.org/?node_id=520116and also
http://hop.perl.plover.com/announce/07although the latter hides some of the magic only for subscribers.
You can
Google for more results.
Now, let's try and see how to convert my recursion based solution into an iterator.
A colleague at work suggested I take a look at
http://en.wikipedia.org/wiki/Permutation#Numbering_permutationsWhat we can learn from that link is basically:
Numbering permutations
Factoradic numbers can be used to assign unique numbers to permutations, such that given a factoradic of k one can quickly find the corresponding permutation.
Algorithm to generate permutations
For every number k (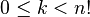 ) this following algorithm generates the corresponding permutation of the initial sequence
) this following algorithm generates the corresponding permutation of the initial sequence 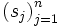 :
:
function permutation(k, s) {
var int factorial:= 1;
for j = 2 to length(s) {
factorial := factorial* (j-1);
swap s[j - ((k / factorial) mod j)] with s[j];
}
return s;
}
Notation
- k / j denotes integer division of k by j, i.e. the integral quotient without any remainder, and
- k mod j is the remainder following integer division of k by j.
So, let's see how this translates to Perl:
sub permute {
my ($k,$s) = @_;
my @list=@$s;
my $factorial= 1;
local $[=1;
for(my $j=2; $j<=@list;++$j) {
$factorial*=($j-1);
my $i=$j-(int($k/$factorial)%$j);
@list[$i,$j]=@list[$j,$i];
}
return @list;
}
Surprisingly, for me, that is, if you iterate over from 1 up to
N!-1 rather than up to
N! the missing permutation will be the original list itself. I wonder if this is a general property of this formulation/solution and how to prove it.
See:
for (1 .. 6) { # 3! equals 6...
print permute($_,[qw(a b c)]),"\n";
}
will produce all permutations, while iterating up to 5 will not produce
[a b c].
I'm still pondering on what kind of refactoring is required in order to turn my recursive implementation into an iterative one, without using algebric tricks like the above mentioned implementation.











































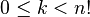 ) this following algorithm generates the corresponding permutation of the initial sequence
) this following algorithm generates the corresponding permutation of the initial sequence 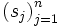 :
: